Movement of flexible salt marsh vegetation under waves
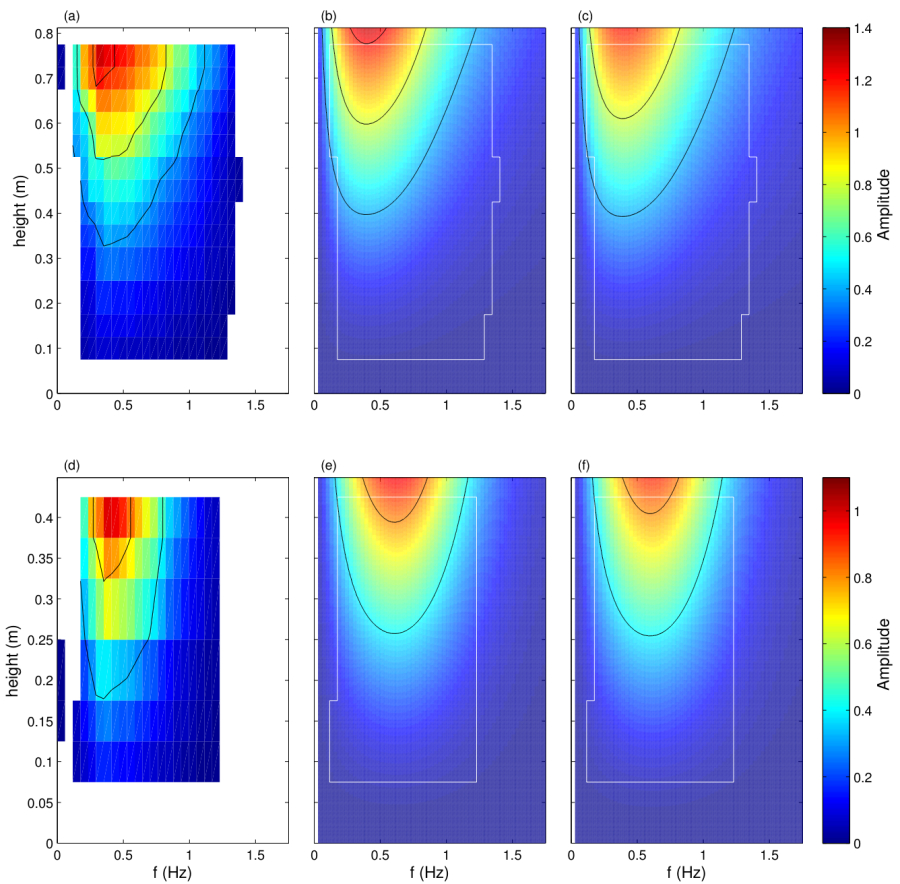
My collaborator Steve Henderson from Washington State University and I developed a new analytical model for the wave-forced movement of single stem vegetation based on the Euler-Bernoulli beam equations. These are more typically used by engineers to find stresses on bridges and other structures! We compared our solutions against filed observations of the motion of sedge (Scheonoplectus americanus) from the Skagit (bay, Washington) salt marsh (see top photo on the left for our field set up). After tuning of a single free parameter (Young’s modulus), the theory successfully predicted the transfer function between measured water and stem motion: See right-hand image for comparison of the observed transfer function on the left with predicted transfer functions on the right (for two different stem geometries). Formulae predicting frequency-dependent wave dissipation by flexible vegetation were derived. It was found that for the moderately flexible stems observed, the model predicted total dissipation was about 30% of the dissipation for equivalent rigid stems – quite a substantial reduction! This work was published in the Journal of Geophysical Research.
To further follow this up, Washington State University masters student Kassi Dallavis compared the Mullarney/Henderson predictions of dissipation to the measured dissipation observed over a natural vegetated salt marsh. She found that the that dissipation was indeed substantially reduced by the tendency of vegetation to bend with the waves, (the photo on the bottom left shows the inside of the array, by which point most wave energy was attenuated). This work has been published in Geophysical Research Letters.